作者:桂。
时间:2017-03-03 23:57:29
链接:

前言
Hilbert通常用来得到解析信号,基于此原理,Hilbert可以用来对窄带信号进行解包络,并求解信号的瞬时频率,但求解包括的时候会出现端点效应,本文对于这几点分别做了简单的理论探讨。
本文内容多有借鉴他人,最后一并附上链接。
一、基本理论
A-Hilbert变换定义
对于一个实信号$x(t)$,其希尔伯特变换为:
$\tilde x(t) = x(t) * \frac{1}{\pi t}$
式中*表示卷积运算。
Hilbert本质上也是转向器,对应频域变换为:
$\frac{1}{
{\pi t}} \Leftrightarrow j\cdot \;sign(\omega )$即余弦信号的Hilbert变换时正弦信号,又有:
$\frac{1}{
{\pi t}}*\frac{1}{ {\pi t}} \Leftrightarrow j \cdot \;sign(\omega ) \cdot j \cdot \;sign(\omega ) = - 1$即信号两次Hilbert变换后是其自身相反数,因此正弦信号的Hilbert是负的余弦。
对应解析信号为:
$z(t) = x(t) + j\tilde x(t)$
此操作实现了信号由双边谱到单边谱的转化。
B-Hilbert解调原理
设有窄带信号:
$x(t) = a(t)\cos [2\pi {f_s}t + \varphi (t)]$
其中$f_s$是载波频率,$a(t)$是$x(t)$的包络,$\varphi (t)$是$x(t)$的相位调制信号。由于$x(t)$是窄带信号,因此$a(t)$也是窄带信号,可设为:
$a(t) = \left[ {1 + \sum\limits_{m = 1}^M {
{X_m}\cos (2\pi {f_m}t + {\gamma _m})} } \right]$式中,$f_m$为调幅信号$a(t)$的频率分量,${\gamma _m}$为$f_m$的各初相角。
对$x(t)$进行Hilbert变换,并求解解析信号,得到:
$z(t) = {e^{j\left[ {2\pi {f_s} + \varphi \left( t \right)} \right]}}\left[ {1 + \sum\limits_{m = 1}^M {
{X_m}\cos (2\pi {f_m}t + {\gamma _m})} } \right]$设
$A(t) = \left[ {1 + \sum\limits_{m = 1}^M {
{X_m}\cos (2\pi {f_m}t + {\gamma _m})} } \right]$$\Phi \left( t \right) = 2\pi {f_s}t + \varphi \left( t \right)$
则解析信号可以重新表达为:
$z(t) = A(t){e^{j\Phi \left( t \right)}}$
对比$x(t)$表达式,容易发现:
$a(t) = A(t) = \sqrt {
{x^2}(t) + { {\tilde x}^2}(t)} $$\varphi (t) = \Phi (t) - 2\pi {f_s}t = \arctan \frac{
{x(t)}}{ {\tilde x(t)}} - 2\pi {f_s}t$由此可以得出:对于窄带信号$x(t)$,利用Hilbert可以求解解析信号,从而得到信号的幅值解调$a(t)$和相位解调$\varphi (t)$,并可以利用相位解调求解频率解调$f(t)$。因为:
$f\left( t \right) = \frac{1}{
{2\pi }}\frac{ {d\varphi (t)}}{ {dt}} = \frac{1}{ {2\pi }}\frac{ {d\Phi (t)}}{ {dt}} - {f_s}$C-相关MATLAB指令
- hilbert
功能:将实数信号x(n)进行Hilbert变换,并得到解析信号z(n).
调用格式:z = hilbert(x)
- instfreq
功能:计算复信号的瞬时频率。
调用格式:[f, t] = insfreq(x,t)
示例:
z = hilbert(x);f = instfreq(z);
二、应用实例
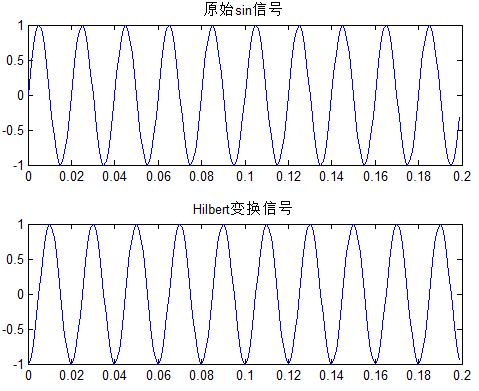
例1:给定一正弦信号,画出其Hilbert信号,直接给代码:
clcclear allclose allts = 0.001;fs = 1/ts;N = 200;f = 50;k = 0:N-1;t = k*ts;% 信号变换% 结论:sin信号Hilbert变换后为cos信号y = sin(2*pi*f*t);yh = hilbert(y); % matlab函数得到信号是合成的复信号yi = imag(yh); % 虚部为书上定义的Hilbert变换figuresubplot(211)plot(t, y)title('原始sin信号')subplot(212)plot(t, yi)title('Hilbert变换信号')ylim([-1,1]) 对应效果图:
例2:已知信号$x(t) = (1 + 0.5\cos (2\pi 5t))\cos (2\pi 50t + 0.5\sin (2\pi 10t))$,求解该信号的包络和瞬时频率。
分析:根据解包络原理知:
信号包络:$(1 + 0.5\cos (2\pi 5t))$
瞬时频率:$\frac{2\pi 50t + 0.5\sin (2\pi 10t)}{2\pi}$
那么问题来了,实际情况是:我们只知道$x(t)$的结果,而不知道其具体表达形式,这个时候,上文的推导就起了作用:可以借助信号的Hilbert变换,从而求解信号的包络和瞬时频率。
对应代码:
clear all; clc; close all;fs=400; % 采样频率N=400; % 数据长度n=0:1:N-1;dt=1/fs;t=n*dt; % 时间序列A=0.5; % 相位调制幅值x=(1+0.5*cos(2*pi*5*t)).*cos(2*pi*50*t+A*sin(2*pi*10*t)); % 信号序列z=hilbert(x'); % 希尔伯特变换a=abs(z); % 包络线fnor=instfreq(z); % 瞬时频率fnor=[fnor(1); fnor; fnor(end)]; % 瞬时频率补齐% 作图pos = get(gcf,'Position');set(gcf,'Position',[pos(1), pos(2)-100,pos(3),pos(4)]);subplot 211; plot(t,x,'k'); hold on;plot(t,a,'r--','linewidth',2); title('包络线'); ylabel('幅值'); xlabel(['时间/s' 10 '(a)']);ylim([-2,2]);subplot 212; plot(t,fnor*fs,'k'); ylim([43 57]);title('瞬时频率'); ylabel('频率/Hz'); xlabel(['时间/s' 10 '(b)']); 其中instfreq为时频工具包的代码,可能有的朋友没有该代码,这里给出其程序:
function [fnormhat,t]=instfreq(x,t,L,trace);%INSTFREQ Instantaneous frequency estimation.% [FNORMHAT,T]=INSTFREQ(X,T,L,TRACE) computes the instantaneous % frequency of the analytic signal X at time instant(s) T, using the% trapezoidal integration rule.% The result FNORMHAT lies between 0.0 and 0.5.% % X : Analytic signal to be analyzed.% T : Time instants (default : 2:length(X)-1).% L : If L=1, computes the (normalized) instantaneous frequency % of the signal X defined as angle(X(T+1)*conj(X(T-1)) ;% if L>1, computes a Maximum Likelihood estimation of the% instantaneous frequency of the deterministic part of the signal% blurried in a white gaussian noise.% L must be an integer (default : 1).% TRACE : if nonzero, the progression of the algorithm is shown% (default : 0).% FNORMHAT : Output (normalized) instantaneous frequency.% T : Time instants.%% Examples : % x=fmsin(70,0.05,0.35,25); [instf,t]=instfreq(x); plot(t,instf)% N=64; SNR=10.0; L=4; t=L+1:N-L; x=fmsin(N,0.05,0.35,40);% sig=sigmerge(x,hilbert(randn(N,1)),SNR);% plotifl(t,[instfreq(sig,t,L),instfreq(x,t)]); grid;% title ('theoretical and estimated instantaneous frequencies');%% See also KAYTTH, SGRPDLAY.% F. Auger, March 1994, July 1995.% Copyright (c) 1996 by CNRS (France).%% ------------------- CONFIDENTIAL PROGRAM -------------------- % This program can not be used without the authorization of its% author(s). For any comment or bug report, please send e-mail to % f.auger@ieee.org if (nargin == 0), error('At least one parameter required');end;[xrow,xcol] = size(x);if (xcol~=1), error('X must have only one column');endif (nargin == 1), t=2:xrow-1; L=1; trace=0.0;elseif (nargin == 2), L = 1; trace=0.0;elseif (nargin == 3), trace=0.0;end;if L<1, error('L must be >=1');end[trow,tcol] = size(t);if (trow~=1), error('T must have only one row'); end;if (L==1), if any(t==1)|any(t==xrow), error('T can not be equal to 1 neither to the last element of X'); else fnormhat=0.5*(angle(-x(t+1).*conj(x(t-1)))+pi)/(2*pi); end;else H=kaytth(L); if any(t<=L)|any(t+L>xrow), error('The relation L <=length(X)-L must be satisfied'); else for icol=1:tcol, if trace, disprog(icol,tcol,10); end; ti = t(icol); tau = 0:L; R = x(ti+tau).*conj(x(ti-tau)); M4 = R(2:L+1).*conj(R(1:L)); diff=2e-6; tetapred = H * (unwrap(angle(-M4))+pi); while tetapred<0.0 , tetapred=tetapred+(2*pi); end; while tetapred>2*pi, tetapred=tetapred-(2*pi); end; iter = 1; while (diff > 1e-6)&(iter<50), M4bis=M4 .* exp(-j*2.0*tetapred); teta = H * (unwrap(angle(M4bis))+2.0*tetapred); while teta<0.0 , teta=(2*pi)+teta; end; while teta>2*pi, teta=teta-(2*pi); end; diff=abs(teta-tetapred); tetapred=teta; iter=iter+1; end; fnormhat(icol,1)=teta/(2*pi); end; end;end; 对应的结果图为:
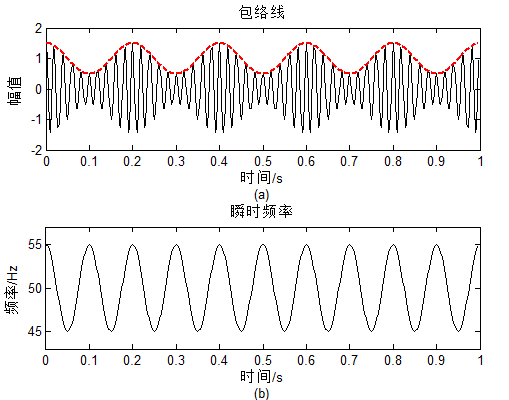
可以看到信号的包络、瞬时频率,均已完成求解。
例3:例2中信号包络为规则的正弦函数,此处给定任意形式的包络(以指数形式为例),并利用Hilbert求解包络以及瞬时频率,并给出对应的Hilbert谱。
程序:
clcclear allclose allts = 0.001;fs = 1/ts;N = 200;k = 0:N-1;t = k*ts;% 原始信号f1 = 10;f2 = 70;% a = cos(2*pi*f1*t); % 包络1a = 2 + exp(0.2*f1*t); % 包络2% a = 1./(1+t.^2*50); % 包络3m = sin(2*pi*f2*t); % 调制信号y = a.*m; % 信号调制figuresubplot(241)plot(t, a)title('包络')subplot(242)plot(t, m)title('调制信号')subplot(243)plot(t, y)title('调制结果')% 包络分析% 结论:Hilbert变换可以有效提取包络、高频调制信号的频率等yh = hilbert(y);aabs = abs(yh); % 包络的绝对值aangle = unwrap(angle(yh)); % 包络的相位af = diff(aangle)/2/pi; % 包络的瞬时频率,差分代替微分计算% NFFT = 2^nextpow2(N);NFFT = 2^nextpow2(1024*4); % 改善栅栏效应f = fs*linspace(0,1,NFFT);YH = fft(yh, NFFT)/N; % Hilbert变换复信号的频谱A = fft(aabs, NFFT)/N; % 包络的频谱subplot(245)plot(t, aabs,'r', t, a)title('包络的绝对值')legend('包络分析结果', '真实包络')subplot(246)plot(t, aangle)title('调制信号的相位')subplot(247)plot(t(1:end-1), af*fs)title('调制信号的瞬时频率')subplot(244)plot(f,abs(YH))title('原始信号的Hilbert谱')xlabel('频率f (Hz)')ylabel('|YH(f)|')subplot(248)plot(f,abs(A))title('包络的频谱')xlabel('频率f (Hz)')ylabel('|A(f)|') 对应结果图:
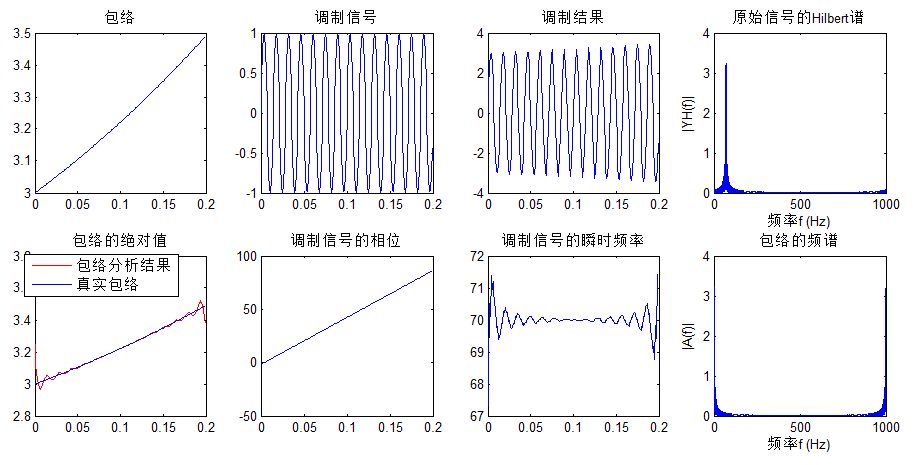
从结果可以观察,出了边界误差较大,结果值符合预期。对于边界效应的分析,见扩展阅读部分。注意:此处瞬时频率求解,没有用instfreq函数,扩展阅读部分对该函数作进一步讨论。
三、扩展阅读
A-瞬时频率求解方法对比
对于离散数据,通常都是用差分代替微分,因此瞬时频率也可根据概念直接求解。此处对比分析两种求解瞬时频率的方法,给出代码:
clcclear allclose allts = 0.001;fs = 1/ts;N = 200;k = 0:N-1;t = k*ts;% 原始信号f1 = 10;f2 = 70;% a = cos(2*pi*f1*t); % 包络1a = 2 + exp(0.2*f1*t); % 包络2% a = 1./(1+t.^2*50); % 包络3m = sin(2*pi*f2*t); % 调制信号y = a.*m; % 信号调制figureyh = hilbert(y);aangle = unwrap(angle(yh)); % 包络的相位af1 = diff(aangle)/2/pi; % 包络的瞬时频率,差分代替微分计算af1 = [af1(1),af1];subplot 211plot(t, af1*fs);hold on;plot(t,70*ones(1,length(t)),'r--','linewidth',2);title('直接求解调制信号的瞬时频率');legend('频率估值','真实值','location','best');subplot 212af2 = instfreq(yh.').';af2 = [af2(1),af2,af2(end)];plot(t, af2*fs);hold on;plot(t,70*ones(1,length(t)),'r--','linewidth',2);title('instfreq求解调制信号的瞬时频率');legend('频率估值','真实值','location','best'); 结果图:
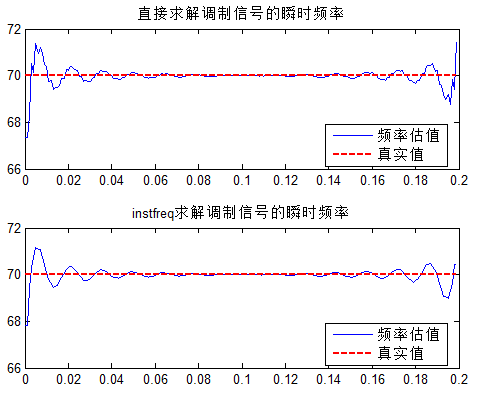
可以看出,两种方式结果近似,但instfreq的结果更为平滑一些。
B-端点效应分析
对于任意包络,求解信号的包络以及瞬时频率,容易出现端点误差较大的情况,该现象主要基于信号中的Gibbs现象,限于篇幅,拟为此单独写一篇文章,具体请参考:。
C-VMD、EMD
Hilbert经典应用总绕不开HHT(Hilbert Huang),HHT基于EMD,近年来又出现了VMD分解,拟为此同样写一篇文章,略说一二心得,具体参考:。
D-解包络方法
需要认识到,Hilbert不是解包络的唯一途径,低通滤波(LPF)等方式一样可以达到该效果,只不过截止频率需要调参。
给出一个Hilbert、低通滤波解包络的代码:
function y=envelope(signal,Fs)%Example:% load('s4.mat');% signal=s4;% Fs=12000;% envelope(signal,Fs);clc;close all;%Normal FFTy=signal;figure();N=2*2048;T=N/Fs;sig_f=abs(fft(y(1:N)',N));sig_n=sig_f/(norm(sig_f));freq_s=(0:N-1)/T;subplot 311plot(freq_s(2:250),sig_n(2:250));title('FFT of Original Signal');%Envelope Detection based on Low pass filter and then FFT[a,b]=butter(2,0.1);%butterworth Filter of 2 poles and Wn=0.1%sig_abs=abs(signal); % Can be used instead of squaring, then filtering and%then taking square rootsig_sq=2*signal.*signal;% squaring for rectifing %gain of 2 for maintianing the same energy in the outputy_sq = filter(a,b,sig_sq); %applying LPFy=sqrt(y_sq);%taking Square root%advantages of taking square and then Square root rather than abs, brings%out some hidden information more efficientlyN=2*2048;T=N/Fs;sig_f=abs(fft(y(1:N)',N));sig_n=sig_f/(norm(sig_f));freq_s=(0:N-1)/T;subplot 312plot(freq_s(2:250),sig_n(2:250));title('Envelope Detection: LPF Method');%Envelope Detection based on Hilbert Transform and then FFTanaly=hilbert(signal);y=abs(analy);N=2*2048;T=N/Fs;sig_f=abs(fft(y(1:N)',N));sig_n=sig_f/(norm(sig_f));freq_s=(0:N-1)/T;subplot 313plot(freq_s(2:250),sig_n(2:250));title('Envelope Detection : Hilbert Transform') 结果图:
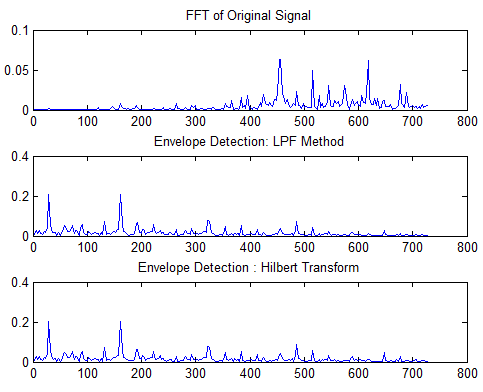
效果是不是也不错?
Hilbert硬件实现思路:
思路1(时域处理):借助MATLAB fdatool实现,Hilbert transform,导出滤波器系数
思路2(频域处理):

参考:
了凡春秋:
宋知用: